

Is it possible that your answers to parts d and e would yield different conclusions? Using a confidence level of 90%, see whether the mean soda price of all your competitors is $2.58 using the p-value. Using a confidence level of 90%, see whether the mean soda price of all your competitors is $2.58 using the t-stat. Calculate the p-value for your t-statistic. Calculate the t-statistic assuming the mean soda price for all of your competitors is $2.58. When conducting data analysis to test this belief, what is this assumption called? 2. You are assuming the mean soda price is $2.58 for all of your competitors. These data are in Soda.xlsx ( See the attached) 1. You know you won't be able to get prices for every restaurant, so you randomly sample 35 and collect their soda prices. To inform your decision, you want to learn more about the average price charged by competing restaurants in the area. You'd like to charge a price equal to the average of your competitors, which you believe is $2.58. Laplace’s and Poissons’s partial differential equations.īeginning with initial guess for the unknowns, 𝑥1 (0) 𝑥2 (0) 𝑥3 (0)Īctivity - You have just opened a restaurant in a large city, and you are deciding what you should charge for a regular-sized soda. The Gauss-Seidel method is used frequently in the solution of Applicable for sparse matrix, i.e., one in which most of the elements Third unknown is determined from the first and second unknowns, Gauss–Seidel method is commonly known as the successiveĭisplacement method is because the second unknown isĭetermined from the first unknown in the current iteration, the Method is named after Carl Friedrich Gauss (Apr 1777–Feb 1855)Īnd Philipp Ludwig von Seidel (Oct 1821–Aug 1896). Gauss–Seidel method is an improved form of Jacobi method. The new iterate depends upon all previously computed Of the linear system of equations, A x = b, one at a time in sequence,Īnd uses previously computed results as soon as they are available. The Gauss-Seidel method is a technique for solving the n equations

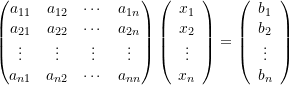
Is an iterative method used to solve a linear system of equations. What mistakes did I make? I think it is in TriSolve method since if I replaced it with regular LU solver such as (np.linalg.solve) it works. In numerical linear algebra, the Gauss–Seidel method, also knownĪs the Liebmann method or the method of successive displacement,

Below is the same implementation in MATLAB which works: function x = gSeidel(A,B,N) For some reason it is not converging even after 50000 iterations to the solution even when the matrix A is strict diagonal dominant. #O(n) per iteration, so overall O(nN), good for large SPD/SDD matricesĪ = np.array(,])Īns = is my Gauss-Seidel method in Python. From scipy.linalg import solve_triangular as triSolve


 0 kommentar(er)
0 kommentar(er)
